二次函数顶点坐标式(它有什么特点)

二次函数顶点坐标式:它有什么特点?

嘿,小伙伴们!今天咱们来聊聊二次函数,没错,就是那个看起来有点像抛物线,又像小山丘的家伙。它可是数学世界里的明星,能描述各种各样的现象,比如抛物线的轨迹、篮球的抛射等等。
想要彻底了解二次函数,就得先掌握它的顶点坐标式,也就是我们今天要深入探讨的主角!
1. 什么是二次函数的顶点坐标式?
咱们来回忆一下,二次函数的标准形式是:y = ax^2 + bx + c。
而顶点坐标式呢?它其实就是把标准形式进行“变形”,把它“打扮”得更简洁,更直观,方便我们一眼就看出它的顶点在哪里。
顶点坐标式长这样:y = a(x - h)^2 + k
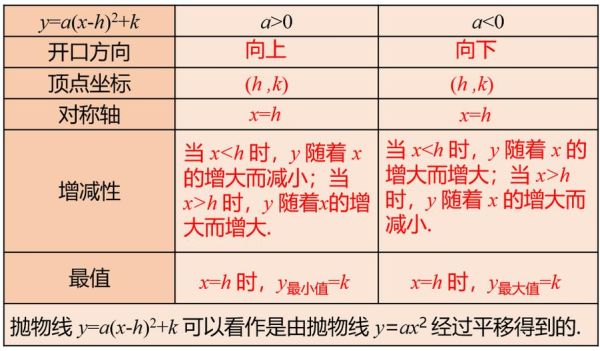
怎么样?是不是看着就舒服多了?
其中,(h, k) 就是二次函数的顶点坐标,也就是抛物线对称轴与抛物线的交点。
举个例子:y = 2(x - 3)^2 + 1,这个函数的顶点坐标就是 (3, 1)。
2. 顶点坐标式有什么用?
顶点坐标式就像二次函数的“身份证”,它能直接告诉我们很多关于函数的信息,比如:
顶点坐标:顾名思义,顶点坐标式最直接的用途就是告诉我们函数的顶点坐标。
对称轴:顶点坐标式中的 h 就代表了对称轴的方程,也就是 x = h。
开口方向:a 的符号决定了函数的开口方向,如果 a > 0,开口向上,如果 a < 0,开口向下。
函数值的最大值或最小值:当函数开口向上时,顶点坐标的纵坐标 k 就是函数的最小值;当函数开口向下时,顶点坐标的纵坐标 k 就是函数的最大值。
所以,顶点坐标式就像一把“万能钥匙”,能轻松解锁二次函数的各种秘密。
3. 顶点坐标式怎么来的?
顶点坐标式是通过配方得到的,简单来说就是把标准形式的二次函数经过“移项、配方、合并同类项”等一系列操作,最终转化成顶点坐标式。
具体步骤如下:
1. 将标准形式 y = ax^2 + bx + c 的右侧提取公因式 a,得到 y = a(x^2 + (b/a)x) + c。
2. 对括号内的 x^2 + (b/a)x 进行配方,配方的方法是:将括号内系数 b/a 的一半平方,也就是 (b/2a)^2,加减到括号内,得到 y = a[x^2 + (b/a)x + (b/2a)^2 - (b/2a)^2] + c。
3. 将括号内前三个项配方,得到 y = a[(x + b/2a)^2 - (b/2a)^2] + c。
4. 展开括号,得到 y = a(x + b/2a)^2 - a(b/2a)^2 + c。
5. 将常数项合并,得到 y = a(x + b/2a)^2 + [c - a(b/2a)^2]。
这样,我们就得到了顶点坐标式:y = a(x - h)^2 + k,其中 h = -b/2a,k = c - a(b/2a)^2。
4. 顶点坐标式怎么用?
知道了顶点坐标式的由来,咱们再来看看它具体怎么用。
假设我们要画出函数 y = x^2 - 4x + 3 的图像,那么我们可以先把它转换成顶点坐标式。
1. 提取公因式 1,得到 y = (x^2 - 4x) + 3。
2. 对括号内进行配方,得到 y = (x^2 - 4x + 4 - 4) + 3。
3. 将括号内前三个项配方,得到 y = (x - 2)^2 - 4 + 3。
4. 合并常数项,得到 y = (x - 2)^2 - 1。
现在,我们就得到了顶点坐标式 y = (x - 2)^2 - 1。
根据顶点坐标式,我们可以直接得出:
顶点坐标为 (2, -1)。
对称轴为 x = 2。
因为 a = 1 > 0,所以开口向上。
这样,我们就轻松地得到了函数的顶点坐标、对称轴和开口方向,画出图像就变得容易多了!
5. 顶点坐标式与其他形式的关系
其实,除了顶点坐标式之外,二次函数还有标准形式和一般式,它们之间是可以互相转换的。
| 形式 | 公式 | 特点 |
|---|---|---|
| 标准形式 | y = ax^2 + bx + c | 直观显示常数项 |
| 一般式 | y = a(x - x1)(x - x2) | 直观显示根 |
| 顶点坐标式 | y = a(x - h)^2 + k | 直观显示顶点坐标 |
理解它们之间的关系,可以帮助我们更灵活地运用二次函数,解决各种
比如,如果你要判断一个二次函数是否经过某一点,那么使用标准形式可能会比较方便;而如果你要寻找函数的最大值或最小值,那么使用顶点坐标式则更加便捷。
怎么样,小伙伴们,通过今天的学习,你对二次函数的顶点坐标式是不是有了更深入的理解呢?
下次再遇到二次函数,别忘了用它强大的顶点坐标式来“武装”自己,这样你就能够轻松应对各种挑战了!
下次咱们来讨论一下,如何利用顶点坐标式来求解二次函数的图像与直线相交的交点,你有什么想法呢?欢迎在评论区留言分享你的观点!

