三角函数的图像与性质(如何才能区分它们)

三角函数图像与性质,你真的懂了吗?
各位同学,好久不见! 今天我们来聊聊三角函数的图像与性质,这可是高中数学里的大块头,也是高考的常客,所以一定要认真学习哦!
1. 三角函数图像,你真的记住了吗?
「三角函数的图像,真的是太重要了!记住了图像,性质就一目了然了。」
这句话,相信很多同学都听过吧?
说真的,图像确实很重要,但是你真的记住了吗?
很多同学会说:「哎呀,我知道sin是那个波浪形的,cos是和sin一样的,就是往左平移了π/2,tan是那个无限多的折线。」
这种理解方式,只能说是表面上的认识。
要想真正理解三角函数的图像,你必须做到:
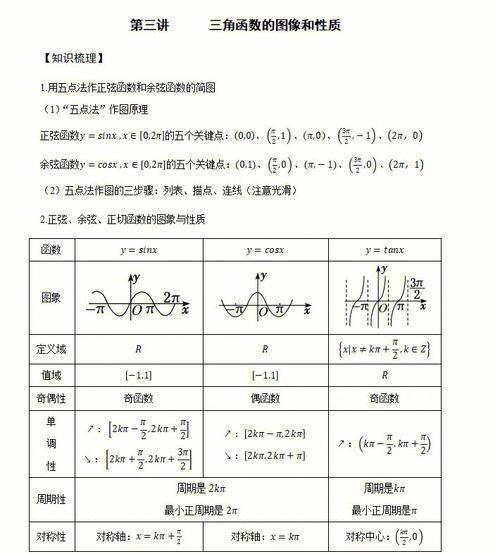
1. 准确画出每个三角函数的图像: 不仅要记住形状,还要注意关键点的坐标,例如:
1. y=sinx 的图像:在[-π,π]上的图像就是一个周期,过点(0,0),(π/2,1),(π,0),(3π/2,-1),(2π,0),并且关于原点对称。
2. y=cosx 的图像:在[-π,π]上的图像就是一个周期,过点(0,1),(π/2,0),(π,-1),(3π/2,0),(2π,1),并且关于y轴对称。
3. y=tanx 的图像:在(-π/2,π/2)上的图像就是一个周期,过点(0,0),并且关于原点对称,在x=-π/2,x=π/2处有垂直渐近线。
2. 理解图像的形成过程: 你可以尝试利用单位圆来理解三角函数图像的形成,这样能够更加深刻地理解三角函数的定义。
3. 理解图像的变换规律: 三角函数图像可以通过平移、伸缩、对称等变换得到新的图像,掌握这些变换规律,能帮助你快速判断一个三角函数图像的性质。
2. 三角函数的性质,你能总结吗?
「三角函数的性质,其实就是图像的另一种表现形式。」
这句话没错,但是你真的能总结出三角函数的所有性质吗?
让我们来回顾一下三角函数的常见性质:
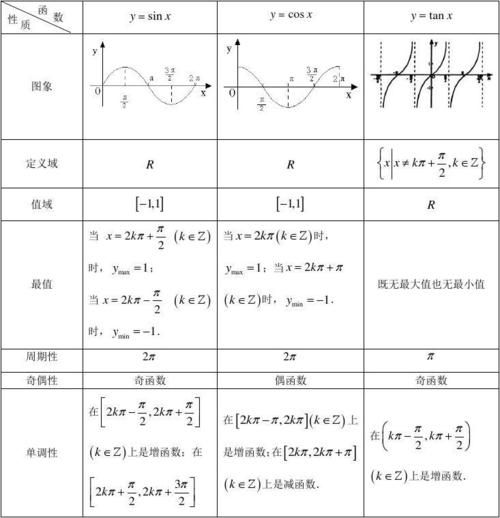
| 性质 | y=sinx | y=cosx | y=tanx |
|---|---|---|---|
| 定义域 | R | R | x≠(k+1/2)π,k∈Z |
| 值域 | [-1,1] | [-1,1] | R |
| 周期 | 2π | 2π | π |
| 奇偶性 | 奇函数 | 偶函数 | 奇函数 |
| 单调性 | 在[-π/2,π/2]上递增,在[π/2,3π/2]上递减 | 在[0,π]上递减,在[π,2π]上递增 | 在(-π/2,π/2)上递增 |
| 对称性 | 关于原点对称 | 关于y轴对称 | 关于原点对称 |
除了这些基本的性质外,还有其他一些重要的性质,例如:
1. 对称性: y=sinx 和 y=tanx 关于原点对称; y=cosx 关于 y 轴对称。
2. 单调性: y=sinx 在[-π/2,π/2]上递增,在[π/2,3π/2]上递减;y=cosx 在[0,π]上递减,在[π,2π]上递增; y=tanx 在(-π/2,π/2)上递增。
3. 最值: y=sinx 和 y=cosx 的最大值为1,最小值为-1。
记住这些性质,你能更方便地分析和解决三角函数相关的题目。
3. 三角函数图像的变换,你掌握了吗?
「三角函数图像的变换,其实就是把一个基本图像进行平移、伸缩、对称等操作,最终得到新的图像。」
这句话听起来很简单,但是实际操作起来,很多同学就犯迷糊了。
常见的三角函数图像变换有以下几种:
1. 平移变换: y=Asin(ωx+φ)+C 或 y=Acos(ωx+φ)+C 的图像,可以通过将 y=sinx 或 y=cosx 的图像进行左右平移和上下平移得到。
1. 左右平移: 当 φ>0 时,图像向左平移 |φ| 个单位;当 φ<0 时,图像向右平移 |φ| 个单位。
2. 上下平移: 当 C>0 时,图像向上平移 C 个单位;当 C<0 时,图像向下平移 |C| 个单位。
2. 伸缩变换: y=Asin(ωx+φ)+C 或 y=Acos(ωx+φ)+C 的图像,可以通过将 y=sinx 或 y=cosx 的图像进行纵向伸缩和横向伸缩得到。
1. 纵向伸缩: 当 A>1 时,图像纵向拉伸,拉伸倍数为 A;当 0 2. 横向伸缩: 当 ω>1 时,图像横向压缩,压缩倍数为 1/ω;当 0<ω<1 时,图像横向拉伸,拉伸倍数为 1/ω。 3. 对称变换: y=Asin(ωx+φ)+C 或 y=Acos(ωx+φ)+C 的图像,可以通过将 y=sinx 或 y=cosx 的图像进行对称变换得到。 1. 关于 x 轴对称: 将 y=sinx 或 y=cosx 的图像关于 x 轴对称,得到 y=-sinx 或 y=-cosx 的图像。 2. 关于 y 轴对称: 将 y=sinx 或 y=cosx 的图像关于 y 轴对称,得到 y=cos(ωx) 或 y=sin(ωx) 的图像。 理解这些变换规律,你能轻松地画出各种三角函数图像,并分析其性质。 4. 三角函数图像与性质的应用,你能举个例子吗? 「三角函数图像与性质,不仅仅是理论知识,它在实际应用中也有着广泛的作用。」 举个例子: 假设你想描述一个物体在竖直方向上的简谐运动,你就可以利用三角函数来建立它的数学模型。 简谐运动是指一个物体在力的作用下,沿着一条直线来回运动,并且其位移随时间变化呈正弦或余弦函数规律。 假设物体的运动规律可以用以下公式描述: y = A\sin(\omega t + φ) 其中: 1. y 表示物体的位移 2. A 表示振幅 3. ω 表示角频率 4. φ 表示初相位 5. t 表示时间 根据这个公式,我们可以画出物体的位移-时间图像,并利用三角函数的性质来分析物体的运动情况。 例如,我们可以知道: 1. 振幅: A 表示物体运动的最大位移。 2. 周期: 物体的周期为 T = 2π/ω,表示物体完成一次完整运动所需的时间。 3. 频率: 物体的频率为 f = 1/T,表示物体每秒钟完成的运动次数。 4. 初相位: φ 表示物体在 t = 0 时刻的位移。 通过分析三角函数图像,我们可以更直观地理解物体运动的规律,并用它来解决实际 5. 如何区分三角函数的图像和性质? 「很多同学会把三角函数的图像和性质搞混,其实只要记住一句话:图像是一幅画,性质是文字描述。」 这句话的意思是,三角函数的图像是一个直观的图形,而性质则是对图像特征的文字描述。 举例说明: y=sinx 图像: 1. 图像: 波浪形的曲线,过原点,在[-π,π]上完成一个周期,关于原点对称。 2. 性质: 定义域为 R,值域为 [-1,1],周期为 2π,奇函数,在 [-π/2,π/2] 上递增,在 [π/2,3π/2] 上递减,关于原点对称。 总结一下,区分三角函数图像和性质的关键是: 1. 图像: 关注的是图形的形状、位置、关键点等直观特征。 2. 性质: 关注的是图形的数学特征,例如定义域、值域、周期、奇偶性、单调性等。 通过理解图像和性质之间的联系,你能更加深刻地理解三角函数的本质。 想问大家一个 你认为除了以上提到的应用外,三角函数图像和性质还有哪些应用?你遇到过哪些与三角函数图像和性质相关的难题?欢迎在评论区留言,分享你的想法和经验!

